| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 헬스
- 아부다비
- 몽골요리
- 파이썬
- 테를지
- 월드프렌즈 ICT 봉사단
- 울란바토르
- 소프트웨어 아카데미
- algorithm
- 초원
- 몽골 고기
- 칭기즈칸
- ICT봉사단
- 몽골 헬스장
- 게르
- 담슈타트
- Python
- 교환학생
- 알고리즘
- 한 줄로 서기
- SWEA
- 칭기스칸 동상
- 백준
- 테를지국립공원
- 월드프렌즈
- LG글로벌챌린저
- 코로나
- 여행
- 독일
- 몽골
- Today
- Total
맛있는물회
[맛있는물회] [파이썬] <백준 알고리즘> 10999번 "구간 합 구하기2" 본문
문제 조건
어떤 N개의 수가 주어져 있다. 그런데 중간에 수의 변경이 빈번히 일어나고 그 중간에 어떤 부분의 합을 구하려 한다. 만약에 1,2,3,4,5 라는 수가 있고, 3번째부터 4번째 수에 6을 더하면 1, 2, 9, 10, 5가 되고, 여기서 2번째부터 5번째까지 합을 구하라고 한다면 26을 출력하면 되는 것이다. 그리고 그 상태에서 1번째부터 3번째 수에 2를 빼고 2번째부터 5번째까지 합을 구하라고 한다면 22가 될 것이다.
Input
첫째 줄에 수의 개수 N(1 ≤ N ≤ 1,000,000)과 M(1 ≤ M ≤ 10,000), K(1 ≤ K ≤ 10,000) 가 주어진다. M은 수의 변경이 일어나는 횟수이고, K는 구간의 합을 구하는 횟수이다. 그리고 둘째 줄부터 N+1번째 줄까지 N개의 수가 주어진다. 그리고 N+2번째 줄부터 N+M+K+1번째 줄까지 세 개의 정수 a, b, c 또는 a, b, c, d가 주어지는데, a가 1인 경우 b번째 수부터 c번째 수에 d를 더하고, a가 2인 경우에는 b부터 c까지의 합을 구하여 출력하면 된다.
입력으로 주어지는 모든 수는 -263보다 크거나 같고, 263-1보다 작거나 같은 정수이다.
Output
첫째 줄부터 K줄에 걸쳐 구한 구간의 합을 출력한다. 단, 정답은 -263보다 크거나 같고, 263-1보다 작거나 같은 정수이다.
생각한 아이디어
진짜 너무너무 어려웠다.
파이썬으로 구현된 코드를 구글링에서 찾기도 힘들었다. 그냥 구글에 포스팅된 파이썬 코드는 없었던 것 같다.
구간 합 구하기 1도 엄청 어려웠는데 2는 더 어렵다...ㅎㅎ
예전에 알고리즘 수업시간에 Heap 에 대해서 배운 기억이 난다.
어떻게 MAX Heap을 update하고 init하고 했는지 기억이 새록새록 난다.
어쨌든 구간 합 구하기는 세그먼트 트리를 이용해서 푸는 방식이다.
이에 대한 설명은
https://blog.naver.com/ndb796/221282210534
https://www.acmicpc.net/blog/view/26
이렇게 참고를 해서 풀었다.
세그먼트 트리와 lazy propagation 알고리즘에 대한 대략적인 이해는 이를 참고하면 좋을 것 같다.
나는 내 코드에 대해서 이해도 제대로 할겸 코드 설명을 좀 해보려 한다.
(아래에 전체 코드가 첨부되어있다)
*메인함수
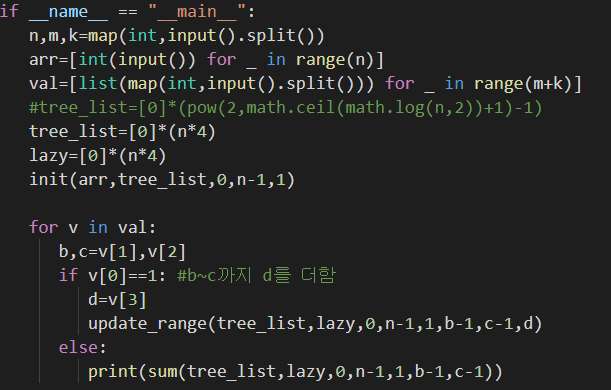
기본적인 입력을 받는 메인 함수이다.

기본적인 트리의 크기를 가지고 트리 리스트를 구성한다.
트리의 크기는 넉넉하게 X4를 해주면 가능하다.
하지만 정확한 크기로 진행하고 싶다면 data값의 길이 n을 기준으로
2^(log(n)+1) - 1으로 수행하면 되겠다.
*init 함수 (트리 초기화)

맨처음에 tree 초기화를 수행하는 함수이다.
start,end는 data의 index이다.
node는 최상위 노드 1부터 쭉 이어짐.
(노드는 data의 인덱스와 달리 0부터 수행하지 않는다. 그 이유는 자식노드를 구할때 node*2, node*2+1 로 쉽게 접근하기 위해서이다)

start == end 라는 의미는 leaf노드라는 의미이다.
따라서 해당 노드에 data의 값을 대입하면 된다.

Leaf 노드가 아니라면 재귀를 수행한다.
재귀를 수행하고 해당 노드에는 자식노드의 값을 더해준다.
*구간합을 구해주는 함수 Sum
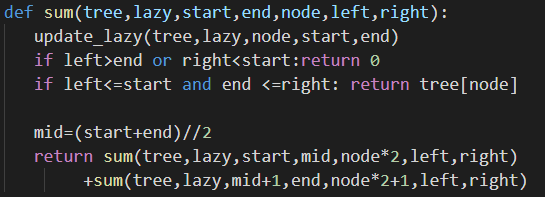
구간합을 구해주는 함수이다.
여기서의 Key Point는 update_lazy이다.
이후에 설명을 하겠지만, sum에서 update_lazy를 해주어야 정상적으로 Lazy Propagation 알고리즘이 작동한다.
즉, lazy Propagation에서 나중에 업데이트한다는 의미가 sum을 구할때 lazy를 적용해준다는 의미이다.

이 또한 조건문으로 원하는 구간과 해당 노드의 구간을 체크한다.
만약 겹치지 않는다면 0을 리턴한다.
전부 포함된다면 해당노드의 값을 리턴해준다.

그게 아니라면 이전의 init과 동일하게 재귀함수를 진행한다.
*범위 update를 해주는 함수 update_range

일반 update가 아니라 구간의 update를 수행한다.
Lazy Propagation 알고리즘을 통해서 구간의 업데이트 에서는 꼭 필요할 때가 오기 전까지는 업데이트를 수행하지 않는다.
쉽게 말해서 해당 노드가 우리가 update하고 싶은 구간을 모두 포함하고 있다면 lazy Propagation을 수행하고,
그게아니라 해당 노드가 update하고 싶은 구간의 일부 부분만을 포함하고 있다면 일반적인 update_range 코드가 수행된다.

이 또한 if 문으로 원하는 구간과 해당 노드의 구간을 비교한다.
위에 적힌대로 수행한다.
만약 일부만 포함한다면 재귀함수를 통해서 다시 update_range를 수행한다.
* lazy 리스트를 통해 update를 해주는 update_lazy

update_lazy는 단순히 lazy의 값만 update하는 것이 아닌 해당 노드에 lazy값이 존재한다면 tree 값도 변경해준다.
그리고 lazy 값을 자식으로 넘겨주면서 propagation이 일어나게 한다.
따라서 이 함수를 update 에만 쓰는 것이 아니라 sum에도 사용하면서 자동으로 lazy를 통하여 update가 propagation되도록 하는 것이다.
사실 아직도 정확하게 로직이 이해되지는 않는다...
계속 풀어봐야 할 것 같다.
파이썬 유저들이 나처럼 구글링을 통해서 코드를 못찾아서 헤매지말고 이 포스팅이 도움이 되었으면 좋겠다!!
건승!
소스코드
#10999 구간 합 구하기2
import sys
import math
from collections import deque
import copy
input=sys.stdin.readline
INF=sys.maxsize
def init(arr,tree,start,end,node):
if start==end:
tree[node]=arr[start]
else:
mid = (start+end)//2
init(arr,tree,start,mid,node*2)
init(arr,tree,mid+1,end,node*2+1)
tree[node]=tree[node*2]+tree[node*2+1]
def update_lazy(tree,lazy,node,start,end):
if lazy[node] !=0:
tree[node] += (end-start+1)*lazy[node]
if start!=end:
lazy[node*2]+=lazy[node]
lazy[node*2+1]+=lazy[node]
lazy[node]=0
def update_range(tree,lazy,start,end,node,idx_start,idx_end,dif):
update_lazy(tree,lazy,node,start,end)
if idx_start>end or start>idx_end: return
if start>=idx_start and idx_end>=end:
tree[node]+=(end-start+1)*dif
if start!=end:
lazy[node*2]+=dif
lazy[node*2+1]+=dif
return
mid = (start+end)//2
update_range(tree,lazy,start,mid,node*2,idx_start,idx_end,dif)
update_range(tree,lazy,mid+1,end,node*2+1,idx_start,idx_end,dif)
tree[node]=tree[node*2]+tree[node*2+1]
def sum(tree,lazy,start,end,node,left,right):
update_lazy(tree,lazy,node,start,end)
if left>end or start>right:return 0
if start>=left and right>=end: return tree[node]
mid=(start+end)//2
return sum(tree,lazy,start,mid,node*2,left,right)+sum(tree,lazy,mid+1,end,node*2+1,left,right)
if __name__ == "__main__":
n,m,k=map(int,input().split())
arr=[int(input()) for _ in range(n)]
val=[list(map(int,input().split())) for _ in range(m+k)]
#tree_list=[0]*(pow(2,math.ceil(math.log(n,2))+1)-1)
tree_list=[0]*(n*4)
lazy=[0]*(n*4)
init(arr,tree_list,0,n-1,1)
for v in val:
b,c=v[1],v[2]
if v[0]==1: #b~c까지 d를 더함
d=v[3]
update_range(tree_list,lazy,0,n-1,1,b-1,c-1,d)
else:
print(sum(tree_list,lazy,0,n-1,1,b-1,c-1))
*파이썬 문법 정리
'IT > 알고리즘' 카테고리의 다른 글
| [맛있는물회] [파이썬] <백준 알고리즘> <삼성기출문제> 13458번 "시험 감독" (2) | 2020.06.08 |
|---|---|
| [맛있는물회] [파이썬] <백준 알고리즘> <삼성기출문제> 13460번 "구슬 탈출2" (0) | 2020.06.08 |
| [맛있는물회] [파이썬] <백준 알고리즘> 10816번 "숫자 카드 2" (0) | 2020.06.08 |
| [맛있는물회] [파이썬] <백준 알고리즘> 9251번 "LCS" (최장 공통 부분 수열 찾기) (0) | 2020.06.05 |
| [맛있는물회] [파이썬] <백준 알고리즘> 6593번 "상범 빌딩" (0) | 2020.06.05 |

